regplane3D: Plotting 3D regression predictions in R

2021-03-19 19 min read tutorials [Denis Cohen Nick Baumann]

The interpretation and presentation of empirical findings from (generalized) linear models has come a long way in the social sciences. Researchers increasingly visualize substantively meaningful quantities of interest such as expected values, first differences, and average marginal effects and consistently include uncertainty estimates in the form of analytical, simulation-based, or bootstrapped confidence intervals. However, existing interpretations and presentations are typically restricted to bivariate patterns which show (changes in) expected values as function of a single predictor, holding all else constant. This can be a significant limitation, especially when substantive inquiries focus on the interplay of two variables in predicting an outcome. To interpret and visualize such applications effectively, researchers must extend their presentations to include a third dimension. In this Methods Bites Tutorial, Denis Cohen and Nick Baumann introduce and showcase the regplane3D package, a tool for plotting 3D regression predictions in R.

After reading this blog post and engaging with the applied examples, readers will be able to:

generate the quantities of interest from regression models, including expected values over a grid of predictor values and their confidence intervals.
plot these quantities in three-dimensional visualizations using regplane3D.

Overview

The regplane3D package
1. Installation
2. Prerequisites
Motivation
Using regplane3D functions
1. plane3D()
2. twoplanes3D()
Conclusion
1. Citation
2. Bug reports and feedback
Further reading

The regplane3D package

The regplane3D package is a convenience wrapper for Karline Soetaert’s plot3D package. regplane3D uses several plot3D functions to produce visually appealing three-dimensional displays of regression estimates with confidence intervals. For example, the package can be used to plot conditional expected values of an outcome variable $Z$ over the joint distribution of two continuous predictors, $X$ and $Y$, i.e., $\mathbb{E}(Z|X,Y)$.

regplane3D (development version 0.1.0) consists of the following functions:

plane3D: Plot a three-dimensional regression prediction with confidence intervals.
twoplanes3D: Plot a three-dimensional regression prediction with two planes, typically separated at a cut point in one of the two horizontal dimensions, with their respective confidence intervals.
heatmap3D: Auxiliary function for adding three-dimensional heatmaps to plots produced by either plane3D or twoplanes3D. These heatmaps show the joint frequency/density distribution of the model predictors represented on the horizontal axes of the plots.
pretty_axis_inputs: Auxiliary function for generating inputs for prediction and plotting to ensure that the grid lines of the perspective box and the lines of the grid lines of the regression planes match.

regplane3D is developed and maintained by Denis Cohen (author, creator) with the help of Nick Baumann (contributor).

Installation

To install the latest development version of regplane3D from GitHub, run:

## devtools
if (!("devtools" %in% installed.packages()))
  install.packages("devtools")
library(devtools)

## regplane3D
if (!("regplane3D" %in% installed.packages()))
  devtools::install_github("denis-cohen/regplane3D")
library(regplane3D)

Prerequisites

The use of regplane3D functions requires that users provide the following inputs:

A vector containing a sequence of values for the first predictor, $X$.
A vector containing a sequence of values for the second predictor, $Y$.
A matrix containing the expected values of $Z$, or an array containing the expected values as well as their lower and upper confidence interval bounds, for all combinations of the specified values for $X$ and $Y$.
Optional: A matrix containing the discretized joint density or joint frequency of $X$ and $Y$.

We illustrate how these inputs can be generated in some applied examples below. For all illustrations, we will use the regplane3D’s internal data set us, a small data set containing information on incumbent vote shares, approval ratings, and economic growth rates in US Presidential Elections between 1948 and 2004. For a documentation of the data, see ?regplane3D::us.

Motivation

A staple of introductory statistics classes is the notion that model predictions from a linear model are no longer represented by line in two dimensions but by a plane in three dimensions once we extend the simple bivariate regression model to include an additional continuous predictor. Graphical representations of model predictions are widespread for the bivariate case. Most commonly, these appear in the form of conditional expected values of an outcome variable as a function of a key predictor while holding other covariates constant. The Figure below exemplifies this by showing the effect of economic growth on incumbent vote shares in US presidential elections, holding incumbents’ approval rating constant at its sample mean.

R code: Estimation, prediction, and visualization

## ---- Estimation ----
mod <- lm(vote ~ growth + approval, dat = us)

## ---- Prediction ----
growth_vals <- seq(-4, 6, length.out = 101L)
pred <- predict.lm(
      mod,
      newdata = data.frame(growth = growth_vals,
                           approval = mean(us$approval)),
      se.fit = TRUE
    )

## ---- Visualization ----
x_lines <-  seq(-4, 6, 2)
y_lines <- seq(40, 60, 5)

## Canvas
plot(
  1,
  1,
  type = 'n',
  main = "Economic Growth and Incumbent Vote Shares",
  axes = F,
  xlab = "Economic Growth",
  ylab = "E[Incumbent Vote Share]",
  ylim = range(y_lines),
  xlim = range(x_lines)
)
axis(2, outer = FALSE)
axis(1)
rect(
  min(x_lines),
  min(y_lines),
  max(x_lines),
  max(y_lines),
  col = "gray95",
  border = NA
)
for (y in y_lines)
  segments(min(x_lines),
           y,
           max(x_lines),
           y,
           col = "white",
           lwd = 2)
for (x in x_lines)
  segments(x,
           min(y_lines),
           x,
           max(y_lines),
           col = "white",
           lwd = 2)

## Prediction
polygon(
  c(growth_vals, rev(growth_vals)),
  c(
    pred$fit + qnorm(.025) * pred$se.fit,
    rev(pred$fit + qnorm(.975) * pred$se.fit)
  ),
  col = adjustcolor("gray30", alpha.f = .2),
  border = NA
)
lines(growth_vals,
      pred$fit,
      lty = 1,
      col = "gray10",
      lwd = 2)
lines(growth_vals,
      pred$fit + qnorm(.025) * pred$se.fit,
      lty = 1,
      col = "gray30")
lines(growth_vals,
      pred$fit + qnorm(.975) * pred$se.fit,
      lty = 1,
      col = "gray30")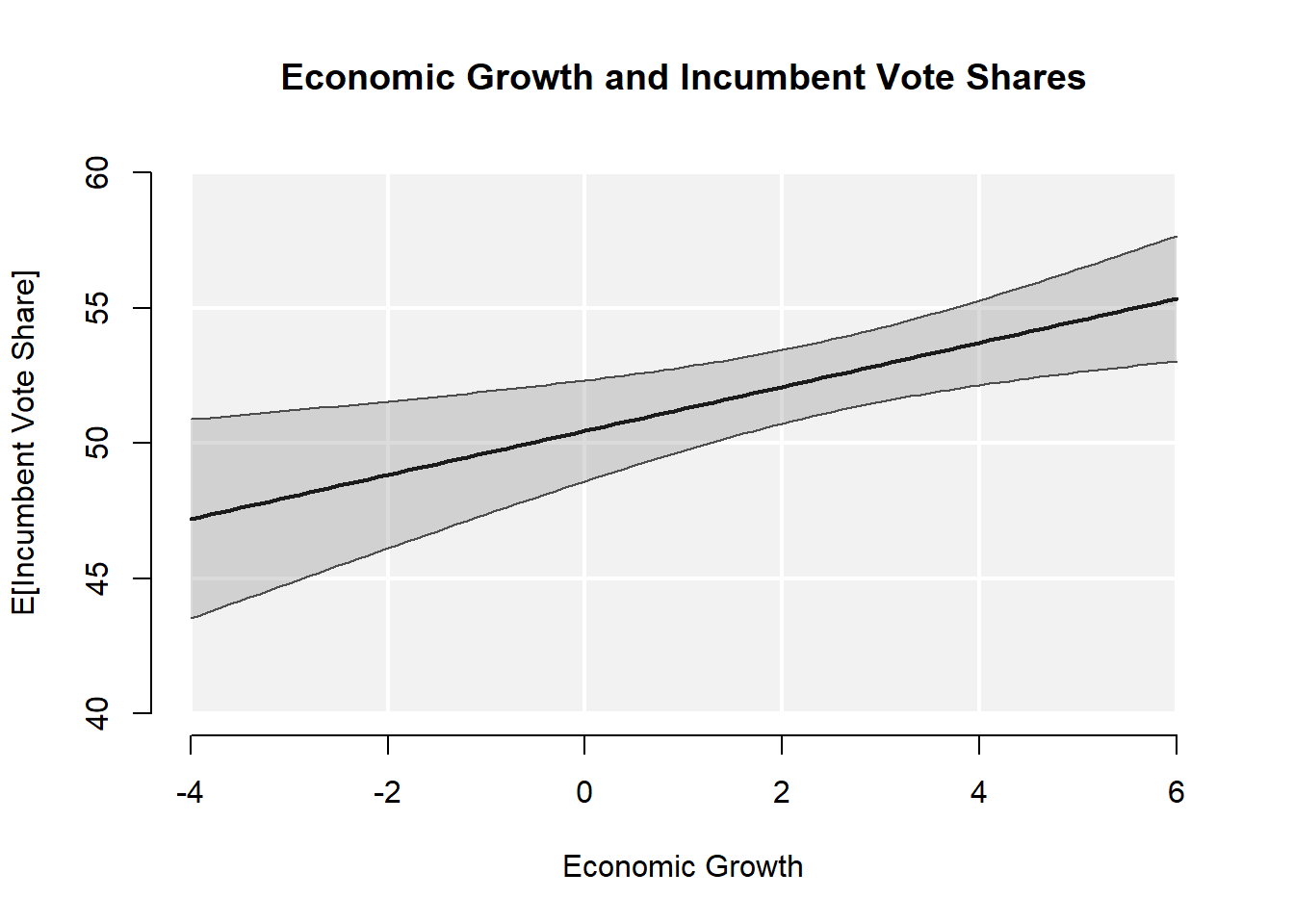

This display of conditional expected values allows readers to grasp at a glance how the expected value of an outcome $Z$ changes along a range of values $\overrightarrow{x}$ of a given predictor $X$. As such, it is both highly informative and easily accessible even to non-technical audiences. Yet, graphically conveying the same information when we want to know how expected values vary as a joint function of two predictors, i.e. $\mathbb{E}[Z | X, Y]$, remains a difficult enterprise. This is especially true when researchers wish to include inferential uncertainty in the form confidence intervals. Among the most common alternatives, researchers typically

separately report marginal effects of $X$ and $Y$ on $Z$, i.e. $\frac{\partial \mathbb{E}[Z | X, Y]}{\partial X}$ and $\frac{\partial \mathbb{E}[Z | X, Y]}{\partial Y}$,
selectively report point estimates of conditional expected at characteristic value pairs $\{x^\prime, y^\prime\}$ of $X$ and $Y$, i.e. $\mathbb{E}[Z | X = x^\prime, Y = y^\prime]$, or
selectively report conditional expected values of $Z$ along a range values $\overrightarrow{x}$ of $X$ while fixing $Y$ at some characteristic value(s) $y^\prime$ (or vice versa), i.e. $\mathbb{E}[Z|X=\overrightarrow{x}, Y=y^\prime]$.

While all of these quantities of interest yield valuable insights into the model-based relationships between the three variables, none of them allows researchers to grasp how the prediction of $\mathbb{E}[Z | X, Y]$ changes over the full grid of plausible value combinations of $X$ and $Y$. This is particularly true if the function that maps $X$ and $Y$ onto $\mathbb{E}[Z | X, Y]$ yields a curved surface.¹ In this case, readers cannot interpolate the full structure of $\mathbb{E}[Z | X, Y]$ from the selective information included in displays generated akin to approaches (2) and (3).

regplane3D offers a flexible toolbox that allows users to overcome these limitations. regplane3D can plot any prediction surface over a two-dimensional grid with two predictors with the corresponding confidence or credible intervals. Users must supply these inputs in the form of an array containing the expected values of $Z$ as well as their lower and upper confidence interval bounds over a grid of pre-specified values of $X$ and $Y$. While this means that users must perform the steps of estimation and prediction before using regplane3D, it also offers users full flexibility with respect to model types, quantities of interest, and method of obtaining uncertainty estimates.

Using regplane3D functions

For the sake of illustration, the following sections will demonstrate the use of regplane3D in the context of conditional expected values from an OLS model with confidence intervals obtained via normal approximation.

plane3D()

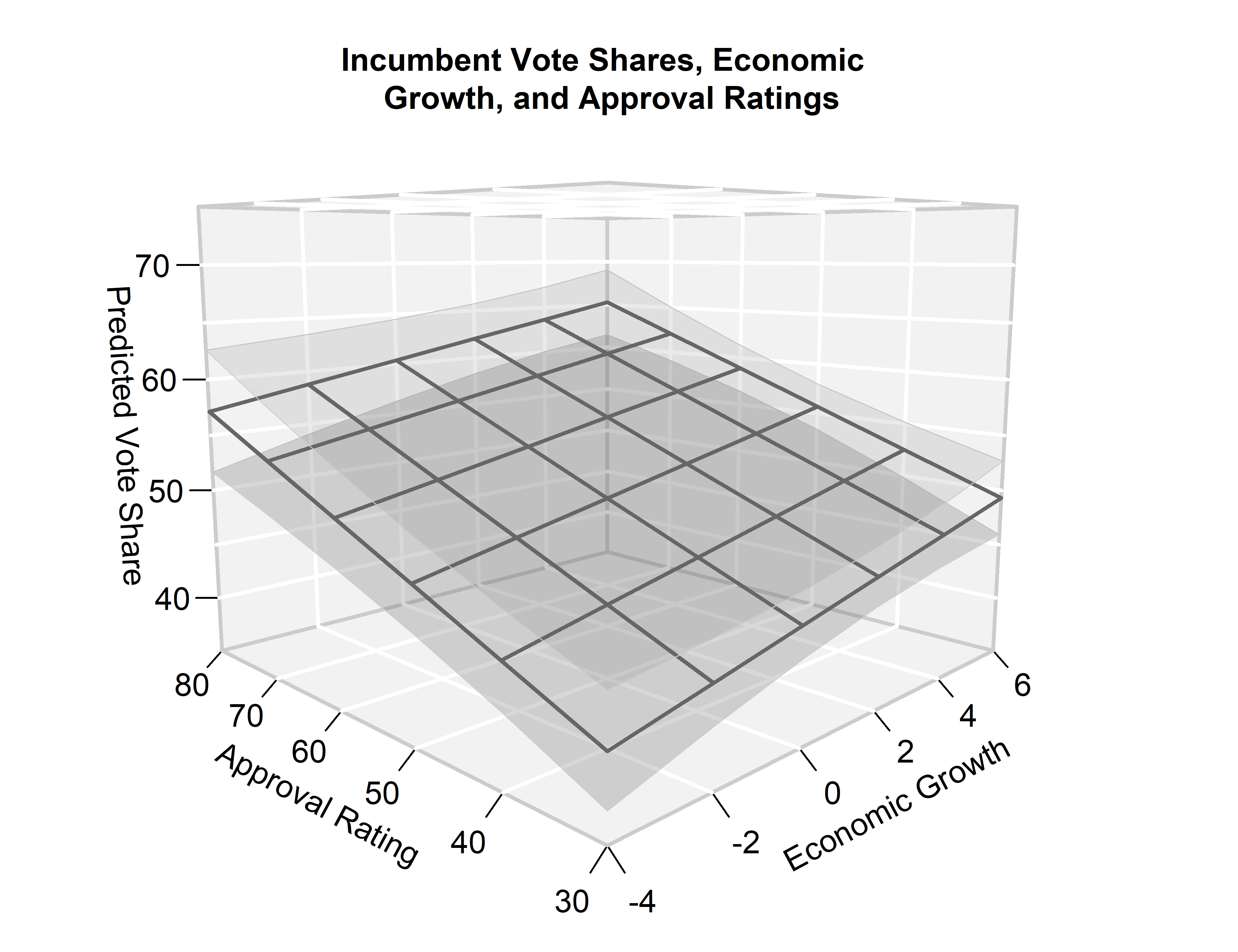
Our first example uses the regplane3D::plane3D() function to illustrate the us in the context of the OLS regression of incumbent vote shares in US Presidential Elections on incumbent approval ratings and economic growth.

Definition of axis inputs

When using regplane3D plotting functions, it is recommended that users use regplane3D::pretty_axis_inputs() for defining axis inputs that should be used for both prediction and plotting. The reason for this requires some explanation. regplane3D plotting functions use plot3D::perspbox() to generate the perspective box inside which the plots are drawn. plot3D::perspbox() in turn depends on graphics::persp(), which uses the base R function base::pretty() to determine the number of ticks and reference lines of the perspective box.

As a result of these dependencies, users have limited control over the exact number and placement of ticks and reference lines. For instance, if users were to provide a variable ranging from 1.89 to 24.31 and request four ticks, this suggestion will be overridden with a rounded value range from 0 to 25 and a total of six ticks in integer steps of 5:

pretty(c(1.89, 24.31), n = 4)

## [1]  0  5 10 15 20 25

Therefore, we recommend that users anticipate this particularity early on and define their axis inputs such that predictions and their visualization eventually conform to the grid lines of the perspective box. The function regplane3D::pretty_axis_inputs() performs these tasks. It rounds value ranges to a custom base and provides the number and positions of the grid lines in the perspective box. These can then be used before the plot is generated to predict the regression plane at the corresponding values. To provide for smoother curves in plots involving curvilinear planes, the option multiply ensure that values of the plane are not only calculated at the intersections of the grid but at finer gradations.

The example below illustrates the functionality. The function extends the range of the variable us$growth (-3.5969999, 5.914) to a base of 2, such that the coarsened range is (-4, 6). We suggest that this range be split into 7 equally spaced intervals. This is rejected by the function, as such a division would not yield pretty values. Instead, the function returns nlines = 6, which means that the lines should be drawn at the reported linevals of -4, -2, 0, 2, 4, and 6. When plotting non-linear relationships, grid lines evaluated at such few values may look a little jerky. To obtain smoother predictions, we can compute our expected values not just at these coarse values but also at finer gradations in between. To accomplish this, we can for instance specify multiply = 4, which means that the linevals sequence in steps of two will be divided into a finer sequence in steps of 0.5, which is returned as seq.

## Find range of variable
growth_range <- range(us$growth)
growth_range

## [1] -3.597  5.914

## Determine axis inputs
growth_axis <- pretty_axis_inputs(
  axis_range = growth_range,
  base = 2,
  nlines_suggest = 7L,
  multiply = 4
)
growth_axis

## $range
## [1] -4  6
## 
## $seq
##  [1] -4.0 -3.5 -3.0 -2.5 -2.0 -1.5 -1.0 -0.5  0.0  0.5  1.0  1.5  2.0  2.5  3.0
## [16]  3.5  4.0  4.5  5.0  5.5  6.0
## 
## $linevals
## [1] -4 -2  0  2  4  6
## 
## $nlines
## [1] 6

Estimation and prediction

To obtain the required inputs, we first run a linear regression model of the form $\texttt{vote} = \beta_1 + \beta_2 \texttt{growth} + \beta_3 \texttt{approval} +\epsilon$ and save the estimation results to an object named mod.

## ---- Estimation ----
mod <- lm(vote ~ growth + approval, dat = us)

We then use regplane3D::pretty_axis_inputs() to define the inputs for both axes. This gives us the sequence of values for each growth and approval.

## ---- Axis inputs ----
## Growth
growth_axis <- pretty_axis_inputs(
  axis_range = range(us$growth),
  base = 2,
  nlines_suggest = 6L,
  multiply = 1
)

## Approval
approval_axis <- pretty_axis_inputs(
  axis_range = range(us$approval),
  base = 10,
  nlines_suggest = 6L,
  multiply = 1
)

For every combination of the values of these two sequences, we subsequently calculate the expected value and the lower and upper bounds of its 95% confidence interval using the predict.lm() function with option se.fit = TRUE. At each iteration of the nested loop, expected values are temporarily stored in pred_tmp$fit and standard errors are temporarily stored in pred_tmp$se.fit. We can extract the expected value and calculate the lower and upper bounds of the 95% confidence interval at each iteration using pred_tmp$fit + qnorm(.025) * pred_tmp$se.fit and pred_tmp$fit + qnorm(.975) * pred_tmp$se.fit, respectively. We subsequently store the estimate of a given iteration in the appropriate cell of the array pred. The array is of dimensions dim = c(length(growth_axis$seq), length(approval_axis$seq), 3L). The first dimension represents the values of growth_axis$seq, the second dimension represents the values of approval_axis$seq, and the third dimension represents the point estimates, lower confidence bounds, and upper confidence bounds.

## ---- Prediction ----
pred <-
  array(NA, dim = c(length(growth_axis$seq), length(approval_axis$seq), 3L))
for (growth in seq_along(growth_axis$seq)) {
  for (approval in seq_along(approval_axis$seq)) {
    pred_tmp <- predict.lm(
      mod,
      newdata = data.frame(growth = growth_axis$seq[growth],
                           approval = approval_axis$seq[approval]),
      se.fit = TRUE
    )
    pred[growth, approval, ] <- c(
      pred_tmp$fit,
      pred_tmp$fit + qnorm(.025) * pred_tmp$se.fit,
      pred_tmp$fit + qnorm(.975) * pred_tmp$se.fit
    )
  }
}

Note: The prediction step can (and should) be adopted to fit the requirements of a given empirical application. For instance, the calculation of expected values from generalized linear models requires the specification of scenarios for the covariate values, the application of an inverse link function, and the use of bootstrapping or parameter simulation for the construction of confidence intervals (though the last step may be skipped in favor of analytical confidence intervals based on normal approximation if the sampling distribution of the quantity of interest is approximately normal). For more information on the calculation of quantities of interest in generalized linear models, see the Further reading section.

Plotting

Using these estimates, we can then plot our regression plane using plane3D(). We pass the inputs z = pred, x = growth_axis$seq, and y = approval_axis$seq to the function, which contain all required information to plot the regression plane. The point estimate of the regression line is plotted by default. Confidence intervals are added per the option cis = TRUE. For additional options, see ?regplane3D::plane3D.

## ---- Plot ----
par(mar = c(2.1, 2.1, 4.1, 0.1))
plane3D(
  z = pred,
  x = growth_axis$seq,
  y = approval_axis$seq,
  zlab = "Predicted Vote Share",
  xlab = "Economic Growth",
  ylab = "Approval Rating",
  zlim = c(35, 75),
  xlim = growth_axis$range,
  ylim = approval_axis$range,
  cis = TRUE,
  xnlines = growth_axis$nlines,
  ynlines = approval_axis$nlines,
  main = "Incumbent Vote Shares, Economic \n Growth, and Approval Ratings",
  theta = -45,
  phi = 9
)

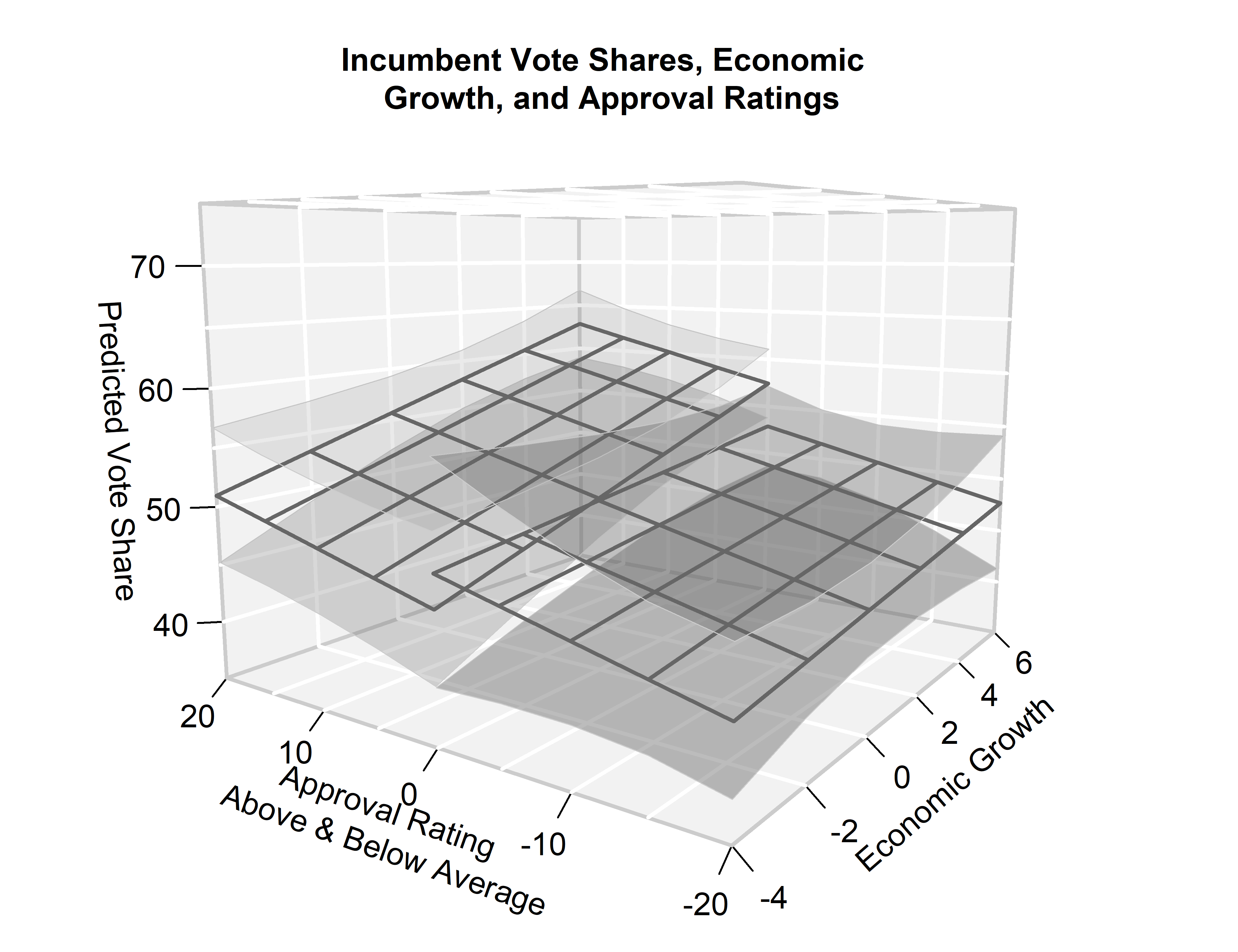
twoplanes3D()

The regplane3D::twoplanes3D() function extends the functionality of regplane3D::plane3D() to accommodate two separate planes. These are typically required when the model prediction is distinct to specific value ranges separated by a cut point in one of the two horizontal dimensions, akin to a discontinuity or binary spline.

We showcase the function by replicating the empirical example introduced above, now with distinct predictions for incumbent presidents with above-average and below-average approval ratings, respectively.

Axis inputs, estimation and prediction

Axis inputs, estimation and prediction are now slightly more intricate than in the previous example. First, we interact both model predictors with the binary indicator approval_above_mean. We then define the axis input for the cut axis (i.e., centered_approval) from its minimum value up to the cut_pointof 0. We store the expected values and confidence bounds across the values of growth_axis$range and approval values ranging from min(centered_approval) up to the cut point of 0 in pred[, , 1, ] for the prediction with below-average approval ratings. Analogously, we store this information for the prediction with above-average approval ratings in pred[, , 2, ], where the values of centered_approval now range from the cut point of up to abs(min(centered_approval)) to provide for a symmetrical value range and display.

R code: Estimation and prediction

## ---- Estimation ----
mod2 <-
  lm(vote ~
       growth +
       centered_approval +
       approval_above_mean +
       growth:approval_above_mean +
       centered_approval:approval_above_mean,
     dat = us)

## ---- Axis inputs ----
## Cut point
cut_point <- 0
approval_above_mean_vals <- c(0, 1)

## Growth
growth_axis2 <- pretty_axis_inputs(
  axis_range = range(us$growth),
  base = 2,
  nlines_suggest = 6L,
  multiply = 1
)

## Approval
approval_axis2 <- pretty_axis_inputs(
  axis_range = c(min(us$centered_approval), cut_point),
  base = 10,
  nlines_suggest = 3L,
  multiply = 1
)

## ---- Prediction ----
pred2 <-
  array(NA, dim = c(length(growth_axis2$seq), length(approval_axis2$seq), 2L, 3L))
for (growth in seq_along(growth_axis2$seq)) {
  for (centered_approval in seq_along(approval_axis2$seq)) {
    for (approval_above_mean in seq_along(approval_above_mean_vals)) {
      pred_tmp <- predict.lm(
        mod2,
        newdata = data.frame(
          growth = growth_axis2$seq[growth],
          centered_approval = approval_axis2$seq[centered_approval] -
            min(approval_axis2$seq) *
            approval_above_mean_vals[approval_above_mean],
          approval_above_mean = approval_above_mean_vals[approval_above_mean]
        ),
        se.fit = TRUE
      )

      pred2[growth, centered_approval, approval_above_mean,] <-
        c(
          pred_tmp$fit,
          pred_tmp$fit + qnorm(.025) * pred_tmp$se.fit,
          pred_tmp$fit + qnorm(.975) * pred_tmp$se.fit
        )
    }
  }
}

Plotting

Plotting with regplane3D::twoplanes3D() works the same way as with regplane3D::plane3D(), except we now must provide the $x$, $y$ and $z$ values separately for both planes. For this, we use the inputs x and x2, y and y2, as well as z and z2.

## ---- Plot ----
par(mar = c(2.1, 2.1, 4.1, 0.1))
twoplanes3D(
  z = pred2[, , 1,],
  x = growth_axis2$seq,
  y = approval_axis2$seq,
  z2 = pred2[, , 2,],
  x2 = growth_axis2$seq,
  y2 = approval_axis2$seq - min(approval_axis2$seq),
  zlim = c(35, 75),
  xlim = growth_axis2$range,
  ylim = c(min(approval_axis2$seq),-min(approval_axis2$seq)),
  zlab = "Predicted Vote Share",
  xlab = "Economic Growth",
  ylab = "Approval Rating \n Above & Below Average",
  cis = TRUE,
  xnlines = growth_axis2$nlines,
  ynlines = approval_axis2$nlines,
  main = "Incumbent Vote Shares, Economic \n Growth, and Approval Ratings",
  theta = -55,
  phi = 9
)

Extensions

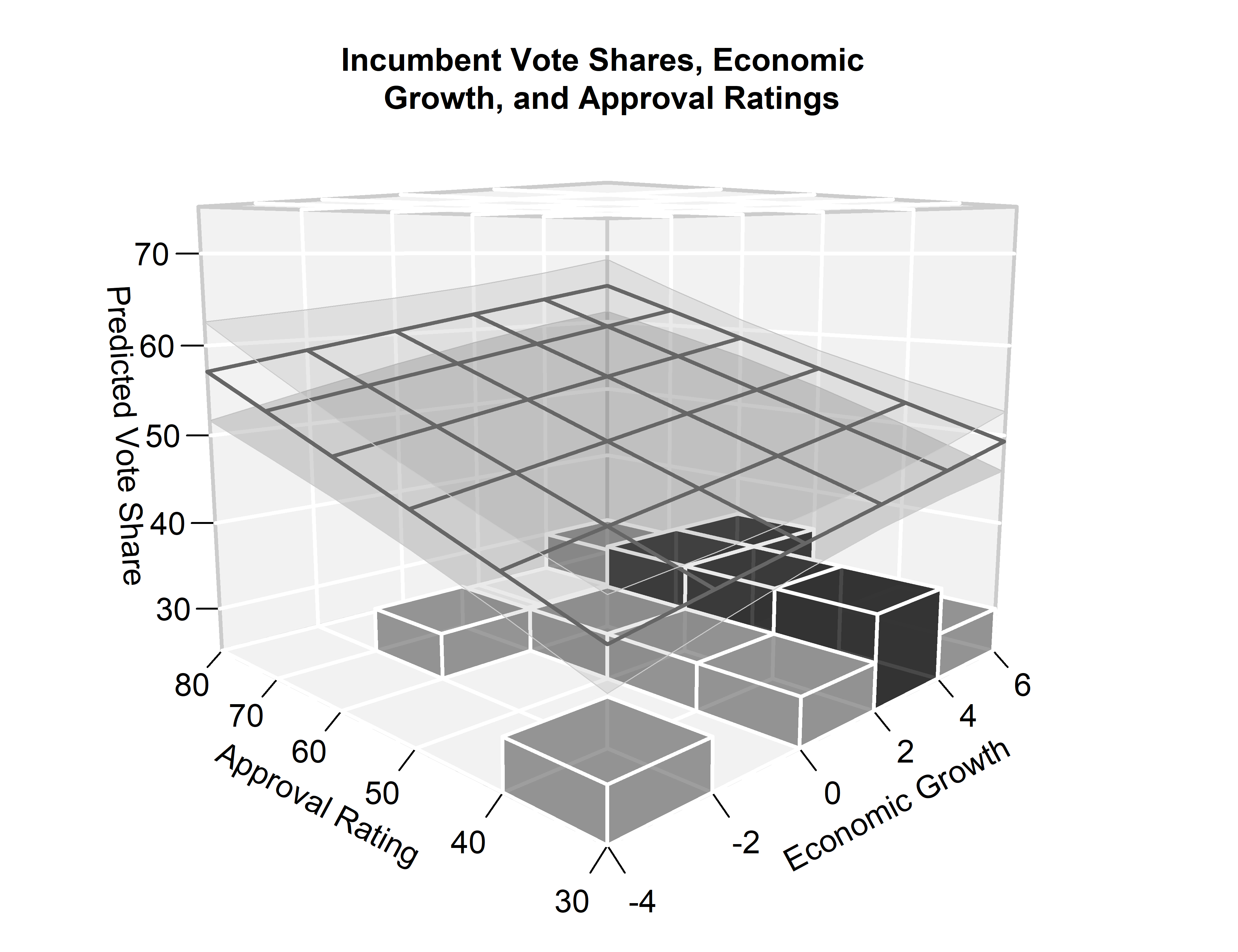
Plot produced with either regplane3D::plane3D() or regplane3D::twoplanes3D() can be extended in numerous ways. For one, we can use regplane3D::heatmap3D() to add a three-dimensional histogram that shows the joint frequency or density distribution of the predictor variables growth and approval. Toward this end, we must first compute a matrix of the joint frequency along discrete intervals of the two continuous predictors. For appealing visuals, it is recommended that the partition of the discrete intervals corresponds to the grid lines of the main plot. These values are returned in the linevals entry of the output returned by regplane3D::pretty_axis_inputs().

## Heatmap values
growth_cat <- cut(us$growth, breaks = growth_axis$linevals)
approval_cat <- cut(us$approval, breaks = approval_axis$linevals)
joint_frequency <- table(growth_cat, approval_cat)

We can then add the three-dimensional heatmap by adding the option heatmap = joint_frequency to our regplane3D::plane3D() command:

## ---- Plot ----
par(mar = c(2.1, 2.1, 4.1, 0.1))
par(mar = c(2.1, 2.1, 4.1, 0.1))
plane3D(
  z = pred,
  x = growth_axis$seq,
  y = approval_axis$seq,
  zlab = "Predicted Vote Share",
  xlab = "Economic Growth",
  ylab = "Approval Rating",
  zlim = c(35, 75),
  xlim = growth_axis$range,
  ylim = approval_axis$range,
  cis = TRUE,
  xnlines = growth_axis$nlines,
  ynlines = approval_axis$nlines,
  main = "Incumbent Vote Shares, Economic \n Growth, and Approval Ratings",
  theta = -45,
  phi = 9,
  heatmap = joint_frequency
)

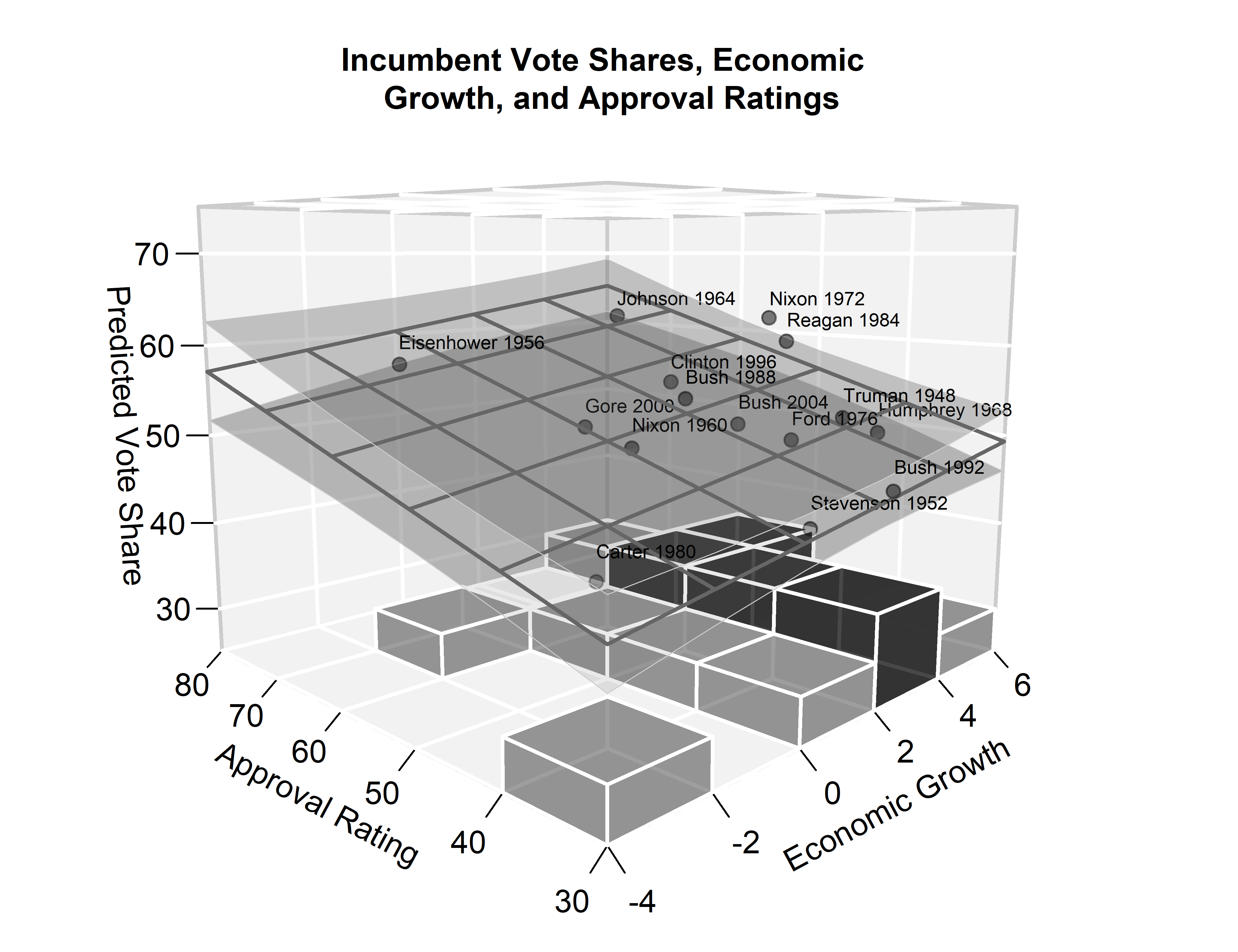
As the regplane3D package is a convenience wrapper for the plot3D package, plots produced by regplane3D plotting functions can be supplemented with output from plot3D functions (using the option add = TRUE). For instance, we can add the observed values of the outcome variable using plot3D::points3D() and add text labels using plot3D::text3D().

## ---- Plot ----
par(mar = c(2.1, 2.1, 4.1, 0.1))
plane3D(
  z = pred,
  x = growth_axis$seq,
  y = approval_axis$seq,
  zlab = "Predicted Vote Share",
  xlab = "Economic Growth",
  ylab = "Approval Rating",
  zlim = c(35, 75),
  xlim = growth_axis$range,
  ylim = approval_axis$range,
  cis = TRUE,
  xnlines = growth_axis$nlines,
  ynlines = approval_axis$nlines,
  main = "Incumbent Vote Shares, Economic \n Growth, and Approval Ratings",
  theta = -45,
  phi = 9,
  heatmap = joint_frequency
)
plot3D::points3D(
  z = us$vote,
  x = us$growth,
  y = us$approval,
  add = TRUE,
  col = adjustcolor("black", alpha.f = .3),
  pch = 19
)
plot3D::text3D(
  z = us$vote + 2.5,
  x = us$growth,
  y = us$approval,
  labels = us$incumbent,
  add = TRUE,
  cex = 0.6
)

Conclusion

An increasing number of empirical applications in quantitative social science focuses on the interplay of two predictors in determining the expected levels of an outcome. Making sense of such analyses requires interpreting the expected values of an outcome variable over the joint distribution of two predictors. Existing visualizations, however, are typically limited to bivariate displays which show the expected values of the outcome variable as a function of a single predictor, fixing the respective other predictor at some characteristic value and holding background covariates constant. To overcome this limitation, this blog post has introduced the regplane3D package and showcased its functionality. Practitioners can now use this tool to produce visually appealing three-dimensional displays of regression estimates with confidence intervals.

Citation

When using regplane3D, please acknowledge the work that has gone into the development of the package and its dependencies.

R code: Package citations

citation("regplane3D")

## 
## To cite package 'regplane3D' in publications use:
## 
##   Denis Cohen (2021). regplane3D: Plotting Regression Predictions in
##   3D. R package version 0.1.0.
##   https://github.com/denis-cohen/regplane3D
## 
## A BibTeX entry for LaTeX users is
## 
##   @Manual{,
##     title = {regplane3D: Plotting Regression Predictions in 3D},
##     author = {Denis Cohen},
##     year = {2021},
##     note = {R package version 0.1.0},
##     url = {https://github.com/denis-cohen/regplane3D},
##   }

citation("plot3D")

## 
## To cite package 'plot3D' in publications use:
## 
##   Karline Soetaert (2019). plot3D: Plotting Multi-Dimensional Data. R
##   package version 1.3. https://CRAN.R-project.org/package=plot3D
## 
## A BibTeX entry for LaTeX users is
## 
##   @Manual{,
##     title = {plot3D: Plotting Multi-Dimensional Data},
##     author = {Karline Soetaert},
##     year = {2019},
##     note = {R package version 1.3},
##     url = {https://CRAN.R-project.org/package=plot3D},
##   }
## 
## ATTENTION: This citation information has been auto-generated from the
## package DESCRIPTION file and may need manual editing, see
## 'help("citation")'.

Bug reports and feedback

regplane3D is still under development. Please feel free to share your feedback, suggest additional features, or flag an issue on GitHub .

About the authors

Denis Cohen is a postdoctoral fellow in the Data and Methods Unit at the Mannheim Centre for European Social Research (MZES), University of Mannheim, and one of the organizers of the MZES Social Science Data Lab. His research focus lies at the intersection of political preference formation, electoral behavior, and political competition. His methodological interests include quantitative approaches to the analysis of clustered data, measurement models, data visualization, strategies for causal identification, and Bayesian statistics.

Nick Baumann is a graduate student in the Mannheim Master of Data Science and a student assistant in the MZES Data and Methods Unit.

When moving beyond the simple case of additive linear regression, we deal with generalized surface structures. For instance, predictions from multivariate linear models that accommodate non-linear relationships or interaction effects as well as predictions from multivariate generalized linear models typically involve surfaces with some curvature. These are generalize flat planes in the same way that curves generalize lines with a constant slope.↩︎